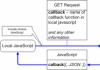
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).
Назначение сервиса . С помощью данного сервиса можно в онлайн режиме решить задачу линейного программирования геометрическим методом, а также получить решение двойственной задачи (оценить оптимальность использования ресурсов). Дополнительно создается шаблон решения в Excel .
Инструкция
. Выберите количество строк (количество ограничений).
Если количество переменных больше двух, необходимо систему привести к СЗЛП (см. и пример №2). Если ограничение двойное, например, 1 ≤ x 1 ≤ 4 , то оно разбивается на два: x 1 ≥ 1 , x 1 ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса .
Вместе с этим калькулятором также используют следующие:
Симплексный метод решения ЗЛП
Решение транспортной задачи
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Экстремум функции двух переменных
Вычисление пределов
Решение задачи линейного программирования графическим методом включает следующие этапы :
- На плоскости X 1 0X 2 строят прямые.
- Определяются полуплоскости.
- Определяют многоугольник решений;
- Строят вектор N(c 1 ,c 2), который указывает направление целевой функции;
- Передвигают прямую целевую функцию c 1 x 2 + c 2 x 2 = 0 в направлении вектора N до крайней точки многоугольника решений.
- Вычисляют координаты точки и значение целевой функции в этой точке.

Пример
. Компания изготавливает два вида продукции - П1 и П2. Для производства продукции используются два вида сырья - С1 и С2. Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.
Таблица - Расход сырья на производство продукции
Требуется определить:
Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
- Сформулировать математическую модель задачи линейного программирования.
- Решить задачу линейного программирования графическим способом (для двух переменных).
Сформулируем математическую модель задачи линейного программирования.
x 1 - производство продукции П1, ед.
x 2 - производство продукции П2, ед.
x 1 , x 2 ≥ 0
Ограничения по ресурсам
6x 1 + 4x 2 ≤ 24
x 1 + 2x 2 ≤ 6
Ограничения по спросу
x 1 +1 ≥ x 2
x 2 ≤ 2
Целевая функция
5x 1 + 4x 2 → max
Тогда получаем следующую ЗЛП:
6x 1 + 4x 2 ≤ 24
x 1 + 2x 2 ≤ 6
x 2 - x 1 ≤ 1
x 2 ≤ 2
x 1 , x 2 ≥ 0
5x 1 + 4x 2 → max
Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП .
→ max при ограничениях:
x 1 + x 2 + x 3 =12
2x 1 - x 2 + x 4 =8
- 2x 1 + 2x 2 + x 5 =10
F(X) = 3x 1 - 2x 2 + 5x 3 - 4x 5
Переход к СЗЛП
.
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
Приведем систему к единичной матрице методом жордановских преобразований.
x 1 + x 2 + x 3 = 12
2x 1 - x 2 + x 4 = 8
- 2x 1 + 2x 2 + x 5 = 10
x 3 = - x 1 - x 2 +12
x 4 = - 2x 1 + x 2 +8
x 5 = 2x 1 - 2x 2 +10
или
Система неравенств:
- x 1 - x 2 +12 ≥ 0
- 2x 1 + x 2 +8 ≥ 0
2x 1 - 2x 2 +10 ≥ 0
x 1 + x 2 ≤ 12
2x 1 - x 2 ≤ 8
- 2x 1 + 2x 2 ≤ 10
Особенности решения задач линейного программирования графическим методом
Пример №1 . Записать задачу в стандартной форме и решить ее графическим методом.f=x 1 +13x 2 -x 3 +2x 4 +3x 5
-x 2 +x 3 -x 5 =-3
x 1 -4x 2 +3x 3 -x 4 +2x 5 =3
4x 2 -x 3 +x 4 -x 5 =6
Из первого уравнения выражаем x 5:
x 5 = -x 2 +x 3 +3
f=x 1 +13x 2 -x 3 +2x 4 +3(-x 2 +x 3 +3)
x 1 -4x 2 +3x 3 -x 4 +2(-x 2 +x 3 +3)=3
4x 2 -x 3 +x 4 -(-x 2 +x 3 +3)=6
или
f=x 1 +10x 2 +2x 3 +2x 4 +9
x 1 -6x 2 +5x 3 -x 4 =-3
5x 2 -2x 3 +x 4 =9
Из второго уравнения выражаем x 4:
x 4 =9-5x 2 +2x 3
и подставим во все выражения:
f=x 1 +6x 3 +27
x 1 -x 2 +3x 3 =6
Переменную x 2 принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x 1 + 6x 3 + 27
x 1 + 3x 3 ≥6
Пример №2
x 1 + x 2 + x 3 =12
2x 1 - x 2 + x 4 =8
- 2x 1 + 2x 2 + x 5 =10
F(X) = 3x 1 - 2x 2 + 5x 3 - 4x 5
Переход к СЗЛП
.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
1. В качестве базовой переменной можно выбрать x 3 .
2. В качестве базовой переменной можно выбрать x 4 .
3. В качестве базовой переменной можно выбрать x 5 .
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x 1 + x 2 + x 3 = 12
2x 1 - x 2 + x 4 = 8
- 2x 1 + 2x 2 + x 5 = 10
Выразим базисные переменные через остальные:
x 3 = - x 1 - x 2 +12
x 4 = - 2x 1 + x 2 +8
x 5 = 2x 1 - 2x 2 +10
Подставим их в целевую функцию:
F(X) = 3x 1 - 2x 2 + 5(- x 1 - x 2 +12) - 4(2x 1 - 2x 2 +10)
или
F(X) = - 10x 1 + x 2 +20 → max
Система неравенств:
- x 1 - x 2 +12 ≥ 0
- 2x 1 + x 2 +8 ≥ 0
2x 1 - 2x 2 +10 ≥ 0
Приводим систему неравенств к следующему виду:
x 1 + x 2 ≤ 12
2x 1 - x 2 ≤ 8
- 2x 1 + 2x 2 ≤ 10
F(X) = - 10x 1 + x 2 +20 → max
Пример №3 . Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
- Составить систему математических зависимостей (неравенств) и целевую функцию.
- Изобразить геометрическую интерпретацию задачи.
- Найти оптимальное решение.
- Провести аналитическую проверку.
- Определить существенные и несущественные ресурсы и их избытки.
- Определить значение целевой функции.
- Вычислить объективно обусловленные оценки.
- Составить соотношение устойчивости.
Если вам понадобится решить задачу линейного программирования с помощью симплекс-таблиц, то наш онлайн сервис вам окажет большую помощь. Симплекс-метод подразумевает последовательный перебор всех вершин области допустимых значений с целью нахождения той вершины, где функция принимает экстремальное значение. На первом этапе находится какое-нибудь решение, которое улучшается на каждом последующем шаге. Такое решение называется базисным. Приведем последовательность действий при решении задачи линейного программирования симплекс-методом:
Первый шаг. В составленной таблице перво-наперво необходимо просмотреть столбец со свободными членами. Если в нем имеются отрицательные элементы, то необходимо осуществить переход ко второму шагу, есле же нет, то к пятому.
Второй шаг. На втором шаге необходимо определиться, какую переменную изключить из базиса, а какую включить, для того, что бы произвести перерасчет симплекс-таблицы. Для этого просматриваем столбец со свободными членами и находим в нем отрицательный элемент. Строка с отрицательным элементом будет называться ведущей. В ней находим максимальный по модулю отрицательный элемент, соответсвующий ему столбец - ведомый. Если же среди свободных членов есть отрицательные значения, а в соответсвующей строке нет, то такая таблица не будет иметь решений. Переменая в ведущей строке, находящаяся в столбце свободных членов исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис.
Таблица 1.
| базисные переменные | Свободные члены в ограничениях | Небазисные переменные | |||||
| x 1 | x 2 | ... | x l | ... | x n | ||
| x n+1 | b 1 | a 11 | a 12 | ... | a 1l | ... | a 1n |
| x n+2 | b 2 | a 21 | a 22 | ... | a 2l | ... | a 2n |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| x n+r | b2 | a r1 | a r2 | ... | a rl | ... | a rn |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| x n+m | b m | a m1 | a m2 | ... | a ml | ... | a mn |
| F(x) max | F 0 | -c 1 | -c 2 | ... | -c 1 | ... | -c n |
Третий шаг. На третьем шаге пересчитываем всю симплекс-таблицу по специальным формулам, эти формулы можно увидеть, воспользовавшись .
Четвертый шаг. Если после перерасчета в столбце свободных членов остались отрицаетельные элементы, то переходим к первому шагу, если таких нет, то к пятому.
Пятый шаг. Если Вы дошли до пятого шага, значит нашли решение, которое допустимо. Однако, это не значит, что оно оптимально. Оптимальным оно будет только в том случае, если положительны все элементы в F-строке. Если же это не так, то необходимо улучшить решение, для чего находим для следующего перерасчета ведущие строку и столбец по следующему алгоритму. Первоначально, находим минимальное отрицательное число в строке F, исключая значение функции. Столбец с этим числом и будем ведущим. Для того, что бы найти ведущую строку, находим отношение соответсвующего свободного члена и элемента из ведущего столбца, при условии, что они положительны. Минимальное отношение позволит определить ведущую строку. Вновь пересчитываем таблицу по формулам, т.е. переходим к шагу 3.
Пример 6.1.

Решение:
Задача линейного программирования задана в стандартной форме и имеет два проектных параметра, следовательно
Воз-можно ее решение геометрическим методом.
1 этап: ( ОДР ).

Рассмотрим первое ограничение, заменим знак неравенства знаком равенства и выразим переменную х2 через х1 :
![]() .
.

Аналогично определяем точки для остальных ограничений системы и строим по ним прямые, соответствующие каждому неравенству (рис. 1). Прямые пронумеруем согласно принятой ранее схеме.
2 этап: .
Определим полуплоскости – решения каждого из неравенств.
Рассмотрим первое неравенство системы ограничений задачи. Возьмем какую-либо точку (контрольную точку), не принадлежащую соответствующей данному неравенству прямой, например, точку (0; 0). Подставим ее в рассматриваемое неравенство:
При подстановке координат контрольной точки неравенство остается справедливым. Следовательно, множество точек, принадлежащих данной прямой (т.к. неравенство не строгое), а также расположенных ниже ее, будут являться решениями рассматриваемого неравенства (пометим на графике (рис. 1) найденную полуплоскость двумя стрелками направленными вниз рядом с прямой I ) .
Аналогично определяем решения других неравенств и соответственно помечаем их графике. В результате график примет следующий вид:
3 этап: .
Найденные полуплоскости (решения каждого из неравенств системы ограничений) при пересечении образуют многоугольник ABCDEO , который и является ОДР рассматриваемой задачи.

Рис. 1. Область допустимых решений задачи
4 этап:
Вектор-градиент показывает направление максимизации целевой функции . Определим его координаты: координаты начальной его точки (точки приложения) – (0; 0), координаты второй точки:
Построим данный вектор на графике (рис. 2).
5 этап: .
Рассмотрим целевую функцию данной задачи:
![]() .
.
Зададим ей какое-либо значение, к примеру, . Выразим переменную х2 через х1 :
![]() .
.
Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:

Построим прямую соответствующую целевой функции (рис. 2).

Рис. 2. Построение целевой функции F(X) и вектора-градиента С
6 этап: определение максимума целевой функ-ции .
Перемещая прямую F (X ) параллельно са-мой себе по направлению вектора-градиента, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 3), такой точкой является точка С – точка пересечения прямых I и II .

Рис. 3. Определение точки максимума целевой функции F(X)
Определим координаты точки С, с этой целью, решим сле-дующую систему линейных уравнений:

Подставим найденные координаты в целевую функцию и найдем ее оптимальное (максимальное) значение:
Ответ: при заданных ограничениях макси-мальное значение целевой функции F (Х )=24, которое достигается в точке С, координаты которой х1 =6, х2 =4.
Пример 6.2. Решить задачу линейного про- граммирования геометрическим методом:
Решение:
Этапы 1-3 аналогичны соответствующим этапам предыдущей задачи.
4 этап: построение вектора-градиента.
Построение вектора-градиента осуществляется аналогично, как и в предыдущей задаче. Построим данный вектор на графике (рис. 4). Отметим также на данном графике стрелкой направление, обратное вектору-градиенту, – направление минимизации целевой функцииF
(X
).
5 этап: построение прямой целевой функ-ции .
Построение прямой целевой функции F (X ) осуществляется аналогично, как и в предыдущей задаче (результат построения приведен на рис. 4).

Рис. 4. Построение целевой функции F(x) и вектора-градиента С
6 этап: определение оптимума целевой функ-ции .
Перемещая прямую F (x ) параллельно са-мой себе в направлении, обратном вектору-градиенту, опреде-ляем крайнюю точку (точки) ОДР. Согласно графику (рис. 5), та- кой точкой является точка О с координатами (0; 0).

Рис. 5. Определение точки минимума целевой функции
Подставляя координаты точки минимума в целевую функ-цию, определяем ее оптимальное (минимальное) значение, которое равно 0.
Ответ:
при заданных ограничениях минимальное значение целевой функции F
(Х
)=0, которое достигается в точке О (0; 0).
Пример 6.3. Решить следующую задачу ли-нейного программирования геометрическим методом:

Решение:
Рассматриваемая задача линейного программирования задана в канонической форме, выделим в качестве базисных переменные x 1 и x 2 .
Составим расширенную матрицу и выделим с помощью метода Жордана- Гаусса базисные переменныеx 1 и x 2 .
![]()
Умножим (поэлементно) первую строку на –3 и сложим со вто-рой:![]() .
.
Умножим вторую строку на :
 .
.
Сложим вторую с первой строкой:
 .
.
В результате система ограничений примет следующий вид:

Выразим базисные переменные через свободные:

Выразим целевую функцию также через свободные перемен-ные, для этого подставим полученные значения базисных переменных в целевую функцию:
Запишем полученную задачу линейного программирования:
![]()

Так как переменные x 1 и x 2 неотрицательные, то полученную систему ограничений можно записать в следующем виде:

Тогда исходную задачу можно записать в виде следующей эк- вивалентной ей стандартной задаче линейного программирования:
![]()

Данная задача имеет два проектных параметра, следовательно, возможно ее решение геометрическим мето-дом.
1 этап: построение прямых, ограничивающих область допустимых решений ( ОДР ).
Рассмотрим систему ограничений задачи линейного програм-мирования (для удобства пронумеруем неравенства):

Построим прямые, соответствующие каждому неравенству (рис. 6). Прямые пронумеруем согласно принятой ранее схе-ме.
2 этап: определение решения каждого из нера-венств системы ограничений .
С помощью контрольных точек определим полуплоскости – решения каждого из неравенств, и пометим их на графике (рис. 6) с помощью стрелок.
3 этап: определение ОДР задачи линейного про- граммирования .
Найденные полуплоскости (т.е. решения каждого из неравенств системы ограничений) не имеют общего пересечения (так решения неравенства I противоречат в целом остальным неравенствам системы ограничений), следовательно, система ограничений не совместна и задача линейного программирования в силу этого не имеет решения.

Рис. 6. Фрагмент MathCAD-документа:
построение области допустимых решений задачи
Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности системы ограничений.
Если после подстановки координат контрольной точки в неравенство его смысл нарушается, то решением данного неравенства является полуплоскость не содержащая данную точку (т.е. расположенная по другую сторону прямой).
Направление, обратное вектору-градиенту, соответствует направлению минимизации целевой функции.
На этом уроке будем знакомиться с графическим методом решения задач линейного программирования , то есть, таких задач, в которых требуется найти такое решения системы линейных уравнений и (или) неравенств (системы ограничений), при котором функция цели - линейная функция - принимает оптимальное значение.
Ввиду того, что наглядность графического решения достигается лишь на плоскости, мы можем познакомиться с графическим представлением задачи только в двумерном пространстве. Это представление пригодно для системы ограничений-неравенств с двумя переменными или для систем уравнений, в которых число переменных на 2 превышает число уравнений, то есть число свободных переменных равно двум.
Поэтому графический метод имеет такие узкие рамки применения, что о нём как об особом методе решения задач линейного программирования говорить нельзя.
Однако для выработки наглядных представлений о решениях задач линейного программирования графический метод представляет определённый интерес. Кроме того, он позволяет геометрически подтвердить справедливость теорем линейного программирования .
Теоретические основы графического метода
Итак, задача линейного программирования. Требуется найти неотрицательные значения переменных и , удовлетворяющих системе неравенств

при которых линейная форма принимает оптимальное значение.
Пример 3.

Пример 4. Решить графическим методом задачу линейного программирования, в которой требуется найти минимум функции при ограничениях

Продолжаем решать задачи графическим методом вместе
До сих пор полученные выводы были основаны на том, что множество решений задачи линейного программирования сконфигурировано так, что оптимальное решение конечно и единственно. Теперь рассмотрим примеры, когда это условие нарушается. В этих примерах многоугольник решений строится так, как показано в предыдущих примерах, остановимся же на признаках, которые отличают эти исключительные примеры.
Пример 5. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях

Решение. На рисунке изображены: неограниченная многогранная область решений данной системы ограничений, исходная линия уровня (чёрного цвета), вектор (бордового цвета), указывающий направление движения исходной линии уровня для нахождения максимума целевой функции.

Легко заметить, что функция F может неограниченно возрастать при заданной системе ограничений, поэтому можно условно записать, что .
Пример 6. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Рассмотрим сначала простейший случай, когда в ЗЛП включены ровно две переменные:
Каждое из неравенств (a)-(b) системы ограничений задачи (3.8) геометрически определяет полуплоскость соответственно с граничными прямыми , Х 1 =0 и Х 2 =0. Каждая из граничных прямых делит плоскость х 1 Ох 2 на две полуплоскости. Все решения исходного неравенства лежат в одной из образованных полуплоскостей (все точки полуплоскости) и, следовательно, при подстановке координат любой ее точки в соответствующее неравенство обращает его в верное тождество. С учетом этого и определяется та полуплоскость, в которой лежат решения неравенства, т.е. путем выбора любой точки из какой-либо полуплоскости и подстановки ее координат в соответствующее неравенство. Если неравенство выполняется для данной точки, то оно выполняется и для любой другой точки из этой же полуплоскости. В противном случае решения неравенства лежат в другой полуплоскости.
В том случае, если система неравенств (a)-(b) совместна, то область её решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей выпуклое, то область допустимых решений задачи (3.8) является выпуклое множество, которое называется многоугольником решений (введённый ранее термин “многогранник решений” обычно употребляется, если n 3). Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.
Таким образом, исходная ЗЛП состоит в нахождении такой точки многоугольника решений, в которой целевая функция F принимает максимальное (минимальное) значение.
Эта точка существует тогда, когда многоугольник решений не пуст и на нём целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины строят линию уровня L: c 1 x 1 +c 2 x 2 =h (где h – некоторая постоянная), перпендикулярную вектору-градиенту и проходящую через многоугольник решений, и передвигают её параллельно вдоль вектора-градиента до тех пор, пока она не пройдёт через последнюю её общую точку пересечения с многоугольником решений (при построении вектора-градиента откладывают точку (с 1 ; с 2) в плоскости х 1 Ох 2 и проводят к ней из начала координат направленный отрезок). Координаты указанной точки и определяют оптимальный план данной задачи.
Суммируя все выше изложенное, приведем алгоритм графического метода решения ЗЛП.
Алгоритм графического метода решения ЗЛП
1. Построить многоугольник решений, задаваемый системой ограничений исходной ЗЛП.
2. Если построенный многоугольник решений – пустое множество, то исходная ЗЛП решений не имеет. В противном случае построить вектор-градиент и провести произвольную линию уровня L, перемещая которую при решении задачи на максимум в направлении вектора (или в обратном направлении для задачи на минимум) определить крайнюю точку многоугольника решений, где и достигается максимум (минимум) целевой функции задачи.
3. Вычислить координаты найденной оптимальной точки , решив систему уравнений двух граничных прямых, пересекающихся в ней.
4. Подстановкой найденного оптимального решения в целевую функцию задачи вычислить оптимальное ее значение, т.е.: .
При графическом построении множества допустимых решений ЗЛП (многоугольника решений) возможны следующие ситуации.